December 2004 43
AT OUR FLYING field awhile ago I met a prospective member
who was waiting for one of our instructors, to have a session with
his 40-size trainer on dual control. He explained that this was his
second model; the first was destroyed when he flew it through a
tree.
While waiting, he watched two club members flying their
electric park flyers, and a funny look appeared on his face. He
realized that he could be learning the basics of flight control on a
much smaller, less-expensive airplane—one that flew slowly
enough to allow errors and recovery without the expense involved
in making the same mistakes on the conventional trainer.
One of the park flyers was also learning—and doing it solo. He
made repeated dunks into the long grass beyond our runway. Each
time the result was his picking up the model, adjusting the wing,
and launching again for another flight. How could that be? The
bigger airplane would almost be destroyed with such handling.
What was going on?
Scaling laws.
Among all of the wonderful laws of physics that bind our
universe are sets of principles known as scaling laws. These are the
relationships that define the effects that size have on physical
behavior. They are fundamental to our hobby and to our everyday
lives.
The primary set of scaling laws of interest to us are sometimes
known as “square-cube” laws, and their first part relates to how an
object’s surface area and volume vary with its size.
Area, Volume, and Weight: An object’s surface area is
proportional to the square of the size. If we double the size, we
increase the surface area by 2 squared: 22 = 4 times. This is true
regardless of the object’s shape.
The volume of this same object, when doubled in size,
increases by 2 cubed: 23 = 8 times. This is also true regardless of
the shape; hence, square-cube laws. Figure 1 depicts these
relationships.
So how is this relevant to our hobby? Bigger models are
heavier than smaller models, judging by much the same factors.
What I am about to explain is simplified to aid in the
understanding of the basic physics; however, as I will show later, it
is close to the real-world application. In fact, the following are the
methods we use in full-scale airplane design.
I’ll begin with a simple example: a solid-balsa model in which
the weight comes entirely from the structure. Let’s assume that we
make a 24-inch-wingspan model of a Staudacher aerobatic model
that weighs 5 ounces. We like it so much that we make a 48-inch
model. Wow! It weighs 40 ounces!
If the 24-inch model weighed 5 ounces and I doubled the size,
I should increase the volume by 2 x 2 x 2 = 8 times. And since I
am still using solid balsa, the density is the same, so the weight
varies by the volume—8 x 5 = 40 ounces. This is depicted in
figure 2.
Great! The scaling laws work. How would a really big model
look? Let’s use twice the 48-inch airplane, or a 96-inch-span
model. Doing the math (2 x 2 x 2 = 8 times), 8 x 40 = 320
ounces, or 20 pounds. That is about right for a big aerobatic
model.
But what if you are not interested in a solid-balsa airplane?
You want to put controls and power in it too. Let’s look at some
real aircraft. Table 1 includes a set of 3-D and aerobatic models
ranging from a light indoor/park flyer to a monster 40%, 122-
inch-span Staudacher.
These airplanes contain all that is necessary for them to fly
under our control. They also have the appropriate structure for
their weight and performance. I plotted them, as shown in Figure
3, to see if there was a trend or relationship between weight and
size.
Figure 1. Scaling Effects on Size, Area, and Volume
Table 1. A family of aerobatic models of increasing size
by Dave Harding
Illustrations by the author
Model
Type
Span—inches
Area—square inches
Weight—ounces
Wing loading—ounces per square foot
Minimum speed—feet per second
Energy—foot pounds
Todd
Long
Tiny
3D
24.0
225.0
3.6
1.4
9.0
1.0
Mountain
Models
Tantrum
3D
37.0
370.0
12.0
4.7
16.0
23.0
Gary
Wright E3D
3D
48.0
600.0
48.0
11.5
24.0
93.0
Magic ARF
3D
52.0
725.0
56.0
11.1
24.0
126.0
Excite
Aerobat
61.0
1,100.0
112.0
14.7
28.0
332.0
Eclipse
Aerobat
79.0
892.0
160.0
25.8
37.0
836.0
Lanier
Edge 540T
Aerobat
90.0
1,474.0
296.0
28.9
39.0
1,731.0
Hangar 9
Extra 300L
Aerobat
97.0
1,750.0
384.0
31.6
41.0
2,453.0
Lanier 40%
Staudacher
Aerobat
122.0
2,474.0
592.0
34.5
42.0
4,124.0
12sig2.QXD 10/25/04 10:33 AM Page 43
factors? Wing loading also increases with size, unless you
deliberately design to reduce it, but that puts you on another trend
line for lighter models; increase them in size and the square-cube
laws apply.
Since weight increases by 9 times and area increases by 4
times, wing loading increases 2.25 times for each doubling of
size. The consequence of this is higher minimum airspeed.
Lift is a function of speed squared, so increasing the wing
loading by 2.25 requires speed to increase by the square root of
2.25—or 1.5—or 50%.
If we combine the effects of increased weight and increased
speed, we find that the kinetic energy in our flying airplane
increases by the astonishing amount of approximately 20 times
with the doubling of a model’s size! This is the energy that must
dissipate when your aircraft lands—or crashes.
Imagine the difference in impact between a 2-pound hammer
and a 40-pound sledgehammer! When your model crashes, this
energy must go somewhere—and much of it goes into breaking
the model! This is why park flyers only bounce.
Power: I started this analysis with a family of 3-D aerobatic
models, and the one essential maneuver for this class of airplane
is hovering flight; let’s examine the impact of scale on power
required to hover.
Figure 2. Effects of Size on Weight
Figure 3
The data plots on a straight-line trend (on log-log scales, but let’s
not get picky because this is the way we do it in the full-scale
world). We even get an equation for the relationship. This is what
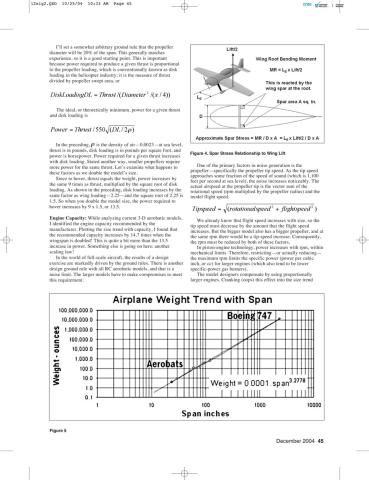
we call a weight trend in airplane design.
The trend equation indicates that span and weight are not related
by the cube power (3), but by 3.22. This is 9 times for a model of
twice the size—not 8. Could this be another factor in the scaling
laws?
For a start, we know from our experience that we need a stronger
structure as we build bigger models. Let’s see.
Stress: Lift is carried on the wing spars. The lift, which is
distributed over the wing, causes stress in the wing-spar caps. For
now, just let’s say that stress is a function of the lift and span. See
Figure 4. The lift is proportional to the model weight and the
maneuver load factor: Gs. In level flight, the lift is equal to the
model weight.
The stress in the spar depends on the spar-cap cross-section area
and the depth of the wing. Stress is defined as the load per unit
area—pounds per square inch in the US.
Let’s apply the scaling laws for a model twice the size. Lift is a
function of weight, and that increased 9 times. The effective span,
LE, and spar depth D are a function of size, and that doubled. The
spar area is size squared; that increases by 4 times.
Therefore, the stress factor is (2 x 9)/(2 x 4) = 2.25.
Working all of this out, you can see that when we double the
model size, the spar stresses are slightly more than double. Since the
allowable stress, or strength, of balsa is fixed (although it does vary
with density), you need a spar material with twice the strength, such
as spruce. This is why you can’t use balsa for spars on larger models
(and you can’t use spruce on even bigger airplanes).
So we have learned that as size increases, we must use stronger,
and therefore heavier, materials to carry the loads. This is one of the
reasons why airplanes actually get heavier by somewhat more than
span3—a factor of 8—each time they double in size; it’s closer to
span3.2—9 times. You can see this in the trend line through the data
from the table overleaf.
Is this real? The Boeing 747 fits on the same trend as the models,
in Figure 5, so there must be something to it, although there are other
factors driving the trend above size cubed. These laws apply in both
directions, so now you can see why the smaller indoor models can
be constructed from rather weak materials such as thin Styrofoam
sheet and lightweight balsa.
Wing Loading, Speed, and Energy: Now we know that airplanes get
disproportionately heavier with size, but what about the other
44 MODEL AVIATION
12sig2.QXD 10/25/04 10:33 AM Page 44
Figure 5
I’ll set a somewhat arbitrary ground rule that the propeller
diameter will be 20% of the span. This generally matches
experience, so it is a good starting point. This is important
because power required to produce a given thrust is proportional
to the propeller loading, which is conventionally known as disk
loading in the helicopter industry; it is the measure of thrust
divided by propeller swept area, or
The ideal, or theoretically minimum, power for a given thrust
and disk loading is
In the preceding, is the density of air—0.0023—at sea level,
thrust is in pounds, disk loading is in pounds per square foot, and
power is horsepower. Power required for a given thrust increases
with disk loading. Stated another way, smaller propellers require
more power for the same thrust. Let’s examine what happens to
these factors as we double the model’s size.
Since to hover, thrust equals the weight, power increases by
the same 9 times as thrust, multiplied by the square root of disk
loading. As shown in the preceding, disk loading increases by the
same factor as wing loading—2.25—and the square root of 2.25 is
1.5. So when you double the model size, the power required to
hover increases by 9 x 1.5, or 13.5.
Engine Capacity: While analyzing current 3-D aerobatic models,
I identified the engine capacity recommended by the
manufacturer. Plotting the size trend with capacity, I found that
the recommended capacity increases by 14.7 times when the
wingspan is doubled! This is quite a bit more than the 13.5
increase in power. Something else is going on here: another
scaling law!
In the world of full-scale aircraft, the results of a design
exercise are markedly driven by the ground rules. There is another
design ground rule with all RC aerobatic models, and that is a
noise limit. The larger models have to make compromises to meet
this requirement.
We already know that flight speed increases with size, so the
tip speed must decrease by the amount that the flight speed
increases. But the bigger model also has a bigger propeller, and at
the same rpm there would be a tip-speed increase. Consequently,
the rpm must be reduced by both of these factors.
In piston-engine technology, power increases with rpm, within
mechanical limits. Therefore, restricting—or actually reducing—
the maximum rpm limits the specific power (power per cubic
inch, or cc) for larger engines (which also tend to be lower
specific-power gas burners).
The model designers compensate by using proportionally
larger engines. Cranking (oops) this effect into the size trend
Figure 4. Spar Stress Relationship to Wing Lift
December 2004 45
One of the primary factors in noise generation is the
propeller—specifically the propeller tip speed. As the tip speed
approaches some fraction of the speed of sound (which is 1,100
feet per second at sea level), the noise increases noticeably. The
actual airspeed at the propeller tip is the vector sum of the
rotational speed (rpm multiplied by the propeller radius) and the
model flight speed:
12sig2.QXD 10/25/04 10:33 AM Page 45
46 MODEL AVIATION
results in the required capacity increasing by the higher 14.7
times for a double-size model.
Maximum Speed: You have seen that the scaling laws drive us to
disproportionately more power as we increase the model size, so
it should be no surprise that this power increase allows the larger
model to go faster.
The typical RC model’s theoretical maximum speed is set by
power and aerodynamic drag. For our “overpowered” models, the
drag at maximum speed is predominantly from wetted area, skin
friction, and form factor, or streamlining.
We conventionally express this drag in terms of the drag
coefficient, or Cd. Drag is related to Cd by a reference area.
Multiplying the Cd by the reference area and multiplying that by
the dynamic pressure calculates the drag. It looks like the
following formula, where the units are pounds, feet, and feet per
second.
For an airplane, the reference area—A—is conventionally the
wing area. Notice that area multiplied by Cd is also an area.
This is sometimes called the “equivalent flat plate drag area,”
because a flat plate with this area, placed perpendicular to the
airstream, would produce roughly the same drag.
Using this concept allows you to estimate the effects of design
changes such as retracting the landing gear, where you would
subtract an area equivalent to the landing-gear frontal area from
the initial equivalent flat plate drag area.
For a given geometry, Cd remains constant with size changes
(excepting the effects defined by that other scaling law discovered
by the good Doctor Reynolds, but we will ignore this for now).
For a given power and drag we can calculate the airspeed
using the following formula, where V is in feet per second and
drag is in pounds.
Substituting the preceding formula for drag, we get the
following, where A is in square feet.
Now you can estimate the effect of doubling size on maximum
speed. When you double the size of the model, the wing area—
and therefore the drag area—increases by 4 times. From my prior
investigation where I doubled the size, the power increased by
13.5 times. Now you see that the speed increase will be
proportional to the cube root of 13.5/4. The speed-increase factor
will be:
So when size increases by a factor of 2, the theoretical
maximum speed increases by a factor of 1.5, which is 50%. I have
called this speed increase “theoretical” because in practice there is
another limiting factor: the propeller. In an aerobatic model,
particularly one that is geared toward 3-D maneuvers, select a
propeller that is aimed at maximizing the hover and low-speed
performance.
Propellers only work well in a narrow speed range. Hover
propellers don’t work at speed. However, if we changed the
propeller for one that optimizes at the maximum speed,
specifically one with the correct smaller diameter and higher
pitch, we should be able to come close to demonstrating the speed
prediction. But propellers are a subject for another time.
Table 2 is a summary of the various scale effects when
doubling a model size or designing a model of a particular scale.
To calculate for a specific scale using a scientific calculator, first
calculate the scale factor as a fraction of roughly the scale in %
divided by 100 (or divide the new span by the baseline).
Second, raise that number to the exponent shown by pressing
the button for xy then pressing the number of the exponent from
the table. The result is the scaling factor you use to multiply the
parameter from your baseline model.
Applying these factors to the 24-inch, 5-ounce balsa
Staudacher and estimating the weight of a 96-inch model:
Weight is 5 x (96/24)3.22 or 5 x 43.22, which is 5 x 86.8 = 434
ounces, or 27 pounds.
Happy scaling. MA
Dave Harding
4948 Jefferson Dr.
Brookhaven PA 19015
Table 2
12sig2.QXD 10/25/04 10:34 AM Page 46
Edition: Model Aviation - 2004/12
Page Numbers: 43,44,45,46
Edition: Model Aviation - 2004/12
Page Numbers: 43,44,45,46
December 2004 43
AT OUR FLYING field awhile ago I met a prospective member
who was waiting for one of our instructors, to have a session with
his 40-size trainer on dual control. He explained that this was his
second model; the first was destroyed when he flew it through a
tree.
While waiting, he watched two club members flying their
electric park flyers, and a funny look appeared on his face. He
realized that he could be learning the basics of flight control on a
much smaller, less-expensive airplane—one that flew slowly
enough to allow errors and recovery without the expense involved
in making the same mistakes on the conventional trainer.
One of the park flyers was also learning—and doing it solo. He
made repeated dunks into the long grass beyond our runway. Each
time the result was his picking up the model, adjusting the wing,
and launching again for another flight. How could that be? The
bigger airplane would almost be destroyed with such handling.
What was going on?
Scaling laws.
Among all of the wonderful laws of physics that bind our
universe are sets of principles known as scaling laws. These are the
relationships that define the effects that size have on physical
behavior. They are fundamental to our hobby and to our everyday
lives.
The primary set of scaling laws of interest to us are sometimes
known as “square-cube” laws, and their first part relates to how an
object’s surface area and volume vary with its size.
Area, Volume, and Weight: An object’s surface area is
proportional to the square of the size. If we double the size, we
increase the surface area by 2 squared: 22 = 4 times. This is true
regardless of the object’s shape.
The volume of this same object, when doubled in size,
increases by 2 cubed: 23 = 8 times. This is also true regardless of
the shape; hence, square-cube laws. Figure 1 depicts these
relationships.
So how is this relevant to our hobby? Bigger models are
heavier than smaller models, judging by much the same factors.
What I am about to explain is simplified to aid in the
understanding of the basic physics; however, as I will show later, it
is close to the real-world application. In fact, the following are the
methods we use in full-scale airplane design.
I’ll begin with a simple example: a solid-balsa model in which
the weight comes entirely from the structure. Let’s assume that we
make a 24-inch-wingspan model of a Staudacher aerobatic model
that weighs 5 ounces. We like it so much that we make a 48-inch
model. Wow! It weighs 40 ounces!
If the 24-inch model weighed 5 ounces and I doubled the size,
I should increase the volume by 2 x 2 x 2 = 8 times. And since I
am still using solid balsa, the density is the same, so the weight
varies by the volume—8 x 5 = 40 ounces. This is depicted in
figure 2.
Great! The scaling laws work. How would a really big model
look? Let’s use twice the 48-inch airplane, or a 96-inch-span
model. Doing the math (2 x 2 x 2 = 8 times), 8 x 40 = 320
ounces, or 20 pounds. That is about right for a big aerobatic
model.
But what if you are not interested in a solid-balsa airplane?
You want to put controls and power in it too. Let’s look at some
real aircraft. Table 1 includes a set of 3-D and aerobatic models
ranging from a light indoor/park flyer to a monster 40%, 122-
inch-span Staudacher.
These airplanes contain all that is necessary for them to fly
under our control. They also have the appropriate structure for
their weight and performance. I plotted them, as shown in Figure
3, to see if there was a trend or relationship between weight and
size.
Figure 1. Scaling Effects on Size, Area, and Volume
Table 1. A family of aerobatic models of increasing size
by Dave Harding
Illustrations by the author
Model
Type
Span—inches
Area—square inches
Weight—ounces
Wing loading—ounces per square foot
Minimum speed—feet per second
Energy—foot pounds
Todd
Long
Tiny
3D
24.0
225.0
3.6
1.4
9.0
1.0
Mountain
Models
Tantrum
3D
37.0
370.0
12.0
4.7
16.0
23.0
Gary
Wright E3D
3D
48.0
600.0
48.0
11.5
24.0
93.0
Magic ARF
3D
52.0
725.0
56.0
11.1
24.0
126.0
Excite
Aerobat
61.0
1,100.0
112.0
14.7
28.0
332.0
Eclipse
Aerobat
79.0
892.0
160.0
25.8
37.0
836.0
Lanier
Edge 540T
Aerobat
90.0
1,474.0
296.0
28.9
39.0
1,731.0
Hangar 9
Extra 300L
Aerobat
97.0
1,750.0
384.0
31.6
41.0
2,453.0
Lanier 40%
Staudacher
Aerobat
122.0
2,474.0
592.0
34.5
42.0
4,124.0
12sig2.QXD 10/25/04 10:33 AM Page 43
factors? Wing loading also increases with size, unless you
deliberately design to reduce it, but that puts you on another trend
line for lighter models; increase them in size and the square-cube
laws apply.
Since weight increases by 9 times and area increases by 4
times, wing loading increases 2.25 times for each doubling of
size. The consequence of this is higher minimum airspeed.
Lift is a function of speed squared, so increasing the wing
loading by 2.25 requires speed to increase by the square root of
2.25—or 1.5—or 50%.
If we combine the effects of increased weight and increased
speed, we find that the kinetic energy in our flying airplane
increases by the astonishing amount of approximately 20 times
with the doubling of a model’s size! This is the energy that must
dissipate when your aircraft lands—or crashes.
Imagine the difference in impact between a 2-pound hammer
and a 40-pound sledgehammer! When your model crashes, this
energy must go somewhere—and much of it goes into breaking
the model! This is why park flyers only bounce.
Power: I started this analysis with a family of 3-D aerobatic
models, and the one essential maneuver for this class of airplane
is hovering flight; let’s examine the impact of scale on power
required to hover.
Figure 2. Effects of Size on Weight
Figure 3
The data plots on a straight-line trend (on log-log scales, but let’s
not get picky because this is the way we do it in the full-scale
world). We even get an equation for the relationship. This is what
we call a weight trend in airplane design.
The trend equation indicates that span and weight are not related
by the cube power (3), but by 3.22. This is 9 times for a model of
twice the size—not 8. Could this be another factor in the scaling
laws?
For a start, we know from our experience that we need a stronger
structure as we build bigger models. Let’s see.
Stress: Lift is carried on the wing spars. The lift, which is
distributed over the wing, causes stress in the wing-spar caps. For
now, just let’s say that stress is a function of the lift and span. See
Figure 4. The lift is proportional to the model weight and the
maneuver load factor: Gs. In level flight, the lift is equal to the
model weight.
The stress in the spar depends on the spar-cap cross-section area
and the depth of the wing. Stress is defined as the load per unit
area—pounds per square inch in the US.
Let’s apply the scaling laws for a model twice the size. Lift is a
function of weight, and that increased 9 times. The effective span,
LE, and spar depth D are a function of size, and that doubled. The
spar area is size squared; that increases by 4 times.
Therefore, the stress factor is (2 x 9)/(2 x 4) = 2.25.
Working all of this out, you can see that when we double the
model size, the spar stresses are slightly more than double. Since the
allowable stress, or strength, of balsa is fixed (although it does vary
with density), you need a spar material with twice the strength, such
as spruce. This is why you can’t use balsa for spars on larger models
(and you can’t use spruce on even bigger airplanes).
So we have learned that as size increases, we must use stronger,
and therefore heavier, materials to carry the loads. This is one of the
reasons why airplanes actually get heavier by somewhat more than
span3—a factor of 8—each time they double in size; it’s closer to
span3.2—9 times. You can see this in the trend line through the data
from the table overleaf.
Is this real? The Boeing 747 fits on the same trend as the models,
in Figure 5, so there must be something to it, although there are other
factors driving the trend above size cubed. These laws apply in both
directions, so now you can see why the smaller indoor models can
be constructed from rather weak materials such as thin Styrofoam
sheet and lightweight balsa.
Wing Loading, Speed, and Energy: Now we know that airplanes get
disproportionately heavier with size, but what about the other
44 MODEL AVIATION
12sig2.QXD 10/25/04 10:33 AM Page 44
Figure 5
I’ll set a somewhat arbitrary ground rule that the propeller
diameter will be 20% of the span. This generally matches
experience, so it is a good starting point. This is important
because power required to produce a given thrust is proportional
to the propeller loading, which is conventionally known as disk
loading in the helicopter industry; it is the measure of thrust
divided by propeller swept area, or
The ideal, or theoretically minimum, power for a given thrust
and disk loading is
In the preceding, is the density of air—0.0023—at sea level,
thrust is in pounds, disk loading is in pounds per square foot, and
power is horsepower. Power required for a given thrust increases
with disk loading. Stated another way, smaller propellers require
more power for the same thrust. Let’s examine what happens to
these factors as we double the model’s size.
Since to hover, thrust equals the weight, power increases by
the same 9 times as thrust, multiplied by the square root of disk
loading. As shown in the preceding, disk loading increases by the
same factor as wing loading—2.25—and the square root of 2.25 is
1.5. So when you double the model size, the power required to
hover increases by 9 x 1.5, or 13.5.
Engine Capacity: While analyzing current 3-D aerobatic models,
I identified the engine capacity recommended by the
manufacturer. Plotting the size trend with capacity, I found that
the recommended capacity increases by 14.7 times when the
wingspan is doubled! This is quite a bit more than the 13.5
increase in power. Something else is going on here: another
scaling law!
In the world of full-scale aircraft, the results of a design
exercise are markedly driven by the ground rules. There is another
design ground rule with all RC aerobatic models, and that is a
noise limit. The larger models have to make compromises to meet
this requirement.
We already know that flight speed increases with size, so the
tip speed must decrease by the amount that the flight speed
increases. But the bigger model also has a bigger propeller, and at
the same rpm there would be a tip-speed increase. Consequently,
the rpm must be reduced by both of these factors.
In piston-engine technology, power increases with rpm, within
mechanical limits. Therefore, restricting—or actually reducing—
the maximum rpm limits the specific power (power per cubic
inch, or cc) for larger engines (which also tend to be lower
specific-power gas burners).
The model designers compensate by using proportionally
larger engines. Cranking (oops) this effect into the size trend
Figure 4. Spar Stress Relationship to Wing Lift
December 2004 45
One of the primary factors in noise generation is the
propeller—specifically the propeller tip speed. As the tip speed
approaches some fraction of the speed of sound (which is 1,100
feet per second at sea level), the noise increases noticeably. The
actual airspeed at the propeller tip is the vector sum of the
rotational speed (rpm multiplied by the propeller radius) and the
model flight speed:
12sig2.QXD 10/25/04 10:33 AM Page 45
46 MODEL AVIATION
results in the required capacity increasing by the higher 14.7
times for a double-size model.
Maximum Speed: You have seen that the scaling laws drive us to
disproportionately more power as we increase the model size, so
it should be no surprise that this power increase allows the larger
model to go faster.
The typical RC model’s theoretical maximum speed is set by
power and aerodynamic drag. For our “overpowered” models, the
drag at maximum speed is predominantly from wetted area, skin
friction, and form factor, or streamlining.
We conventionally express this drag in terms of the drag
coefficient, or Cd. Drag is related to Cd by a reference area.
Multiplying the Cd by the reference area and multiplying that by
the dynamic pressure calculates the drag. It looks like the
following formula, where the units are pounds, feet, and feet per
second.
For an airplane, the reference area—A—is conventionally the
wing area. Notice that area multiplied by Cd is also an area.
This is sometimes called the “equivalent flat plate drag area,”
because a flat plate with this area, placed perpendicular to the
airstream, would produce roughly the same drag.
Using this concept allows you to estimate the effects of design
changes such as retracting the landing gear, where you would
subtract an area equivalent to the landing-gear frontal area from
the initial equivalent flat plate drag area.
For a given geometry, Cd remains constant with size changes
(excepting the effects defined by that other scaling law discovered
by the good Doctor Reynolds, but we will ignore this for now).
For a given power and drag we can calculate the airspeed
using the following formula, where V is in feet per second and
drag is in pounds.
Substituting the preceding formula for drag, we get the
following, where A is in square feet.
Now you can estimate the effect of doubling size on maximum
speed. When you double the size of the model, the wing area—
and therefore the drag area—increases by 4 times. From my prior
investigation where I doubled the size, the power increased by
13.5 times. Now you see that the speed increase will be
proportional to the cube root of 13.5/4. The speed-increase factor
will be:
So when size increases by a factor of 2, the theoretical
maximum speed increases by a factor of 1.5, which is 50%. I have
called this speed increase “theoretical” because in practice there is
another limiting factor: the propeller. In an aerobatic model,
particularly one that is geared toward 3-D maneuvers, select a
propeller that is aimed at maximizing the hover and low-speed
performance.
Propellers only work well in a narrow speed range. Hover
propellers don’t work at speed. However, if we changed the
propeller for one that optimizes at the maximum speed,
specifically one with the correct smaller diameter and higher
pitch, we should be able to come close to demonstrating the speed
prediction. But propellers are a subject for another time.
Table 2 is a summary of the various scale effects when
doubling a model size or designing a model of a particular scale.
To calculate for a specific scale using a scientific calculator, first
calculate the scale factor as a fraction of roughly the scale in %
divided by 100 (or divide the new span by the baseline).
Second, raise that number to the exponent shown by pressing
the button for xy then pressing the number of the exponent from
the table. The result is the scaling factor you use to multiply the
parameter from your baseline model.
Applying these factors to the 24-inch, 5-ounce balsa
Staudacher and estimating the weight of a 96-inch model:
Weight is 5 x (96/24)3.22 or 5 x 43.22, which is 5 x 86.8 = 434
ounces, or 27 pounds.
Happy scaling. MA
Dave Harding
4948 Jefferson Dr.
Brookhaven PA 19015
Table 2
12sig2.QXD 10/25/04 10:34 AM Page 46
Edition: Model Aviation - 2004/12
Page Numbers: 43,44,45,46
December 2004 43
AT OUR FLYING field awhile ago I met a prospective member
who was waiting for one of our instructors, to have a session with
his 40-size trainer on dual control. He explained that this was his
second model; the first was destroyed when he flew it through a
tree.
While waiting, he watched two club members flying their
electric park flyers, and a funny look appeared on his face. He
realized that he could be learning the basics of flight control on a
much smaller, less-expensive airplane—one that flew slowly
enough to allow errors and recovery without the expense involved
in making the same mistakes on the conventional trainer.
One of the park flyers was also learning—and doing it solo. He
made repeated dunks into the long grass beyond our runway. Each
time the result was his picking up the model, adjusting the wing,
and launching again for another flight. How could that be? The
bigger airplane would almost be destroyed with such handling.
What was going on?
Scaling laws.
Among all of the wonderful laws of physics that bind our
universe are sets of principles known as scaling laws. These are the
relationships that define the effects that size have on physical
behavior. They are fundamental to our hobby and to our everyday
lives.
The primary set of scaling laws of interest to us are sometimes
known as “square-cube” laws, and their first part relates to how an
object’s surface area and volume vary with its size.
Area, Volume, and Weight: An object’s surface area is
proportional to the square of the size. If we double the size, we
increase the surface area by 2 squared: 22 = 4 times. This is true
regardless of the object’s shape.
The volume of this same object, when doubled in size,
increases by 2 cubed: 23 = 8 times. This is also true regardless of
the shape; hence, square-cube laws. Figure 1 depicts these
relationships.
So how is this relevant to our hobby? Bigger models are
heavier than smaller models, judging by much the same factors.
What I am about to explain is simplified to aid in the
understanding of the basic physics; however, as I will show later, it
is close to the real-world application. In fact, the following are the
methods we use in full-scale airplane design.
I’ll begin with a simple example: a solid-balsa model in which
the weight comes entirely from the structure. Let’s assume that we
make a 24-inch-wingspan model of a Staudacher aerobatic model
that weighs 5 ounces. We like it so much that we make a 48-inch
model. Wow! It weighs 40 ounces!
If the 24-inch model weighed 5 ounces and I doubled the size,
I should increase the volume by 2 x 2 x 2 = 8 times. And since I
am still using solid balsa, the density is the same, so the weight
varies by the volume—8 x 5 = 40 ounces. This is depicted in
figure 2.
Great! The scaling laws work. How would a really big model
look? Let’s use twice the 48-inch airplane, or a 96-inch-span
model. Doing the math (2 x 2 x 2 = 8 times), 8 x 40 = 320
ounces, or 20 pounds. That is about right for a big aerobatic
model.
But what if you are not interested in a solid-balsa airplane?
You want to put controls and power in it too. Let’s look at some
real aircraft. Table 1 includes a set of 3-D and aerobatic models
ranging from a light indoor/park flyer to a monster 40%, 122-
inch-span Staudacher.
These airplanes contain all that is necessary for them to fly
under our control. They also have the appropriate structure for
their weight and performance. I plotted them, as shown in Figure
3, to see if there was a trend or relationship between weight and
size.
Figure 1. Scaling Effects on Size, Area, and Volume
Table 1. A family of aerobatic models of increasing size
by Dave Harding
Illustrations by the author
Model
Type
Span—inches
Area—square inches
Weight—ounces
Wing loading—ounces per square foot
Minimum speed—feet per second
Energy—foot pounds
Todd
Long
Tiny
3D
24.0
225.0
3.6
1.4
9.0
1.0
Mountain
Models
Tantrum
3D
37.0
370.0
12.0
4.7
16.0
23.0
Gary
Wright E3D
3D
48.0
600.0
48.0
11.5
24.0
93.0
Magic ARF
3D
52.0
725.0
56.0
11.1
24.0
126.0
Excite
Aerobat
61.0
1,100.0
112.0
14.7
28.0
332.0
Eclipse
Aerobat
79.0
892.0
160.0
25.8
37.0
836.0
Lanier
Edge 540T
Aerobat
90.0
1,474.0
296.0
28.9
39.0
1,731.0
Hangar 9
Extra 300L
Aerobat
97.0
1,750.0
384.0
31.6
41.0
2,453.0
Lanier 40%
Staudacher
Aerobat
122.0
2,474.0
592.0
34.5
42.0
4,124.0
12sig2.QXD 10/25/04 10:33 AM Page 43
factors? Wing loading also increases with size, unless you
deliberately design to reduce it, but that puts you on another trend
line for lighter models; increase them in size and the square-cube
laws apply.
Since weight increases by 9 times and area increases by 4
times, wing loading increases 2.25 times for each doubling of
size. The consequence of this is higher minimum airspeed.
Lift is a function of speed squared, so increasing the wing
loading by 2.25 requires speed to increase by the square root of
2.25—or 1.5—or 50%.
If we combine the effects of increased weight and increased
speed, we find that the kinetic energy in our flying airplane
increases by the astonishing amount of approximately 20 times
with the doubling of a model’s size! This is the energy that must
dissipate when your aircraft lands—or crashes.
Imagine the difference in impact between a 2-pound hammer
and a 40-pound sledgehammer! When your model crashes, this
energy must go somewhere—and much of it goes into breaking
the model! This is why park flyers only bounce.
Power: I started this analysis with a family of 3-D aerobatic
models, and the one essential maneuver for this class of airplane
is hovering flight; let’s examine the impact of scale on power
required to hover.
Figure 2. Effects of Size on Weight
Figure 3
The data plots on a straight-line trend (on log-log scales, but let’s
not get picky because this is the way we do it in the full-scale
world). We even get an equation for the relationship. This is what
we call a weight trend in airplane design.
The trend equation indicates that span and weight are not related
by the cube power (3), but by 3.22. This is 9 times for a model of
twice the size—not 8. Could this be another factor in the scaling
laws?
For a start, we know from our experience that we need a stronger
structure as we build bigger models. Let’s see.
Stress: Lift is carried on the wing spars. The lift, which is
distributed over the wing, causes stress in the wing-spar caps. For
now, just let’s say that stress is a function of the lift and span. See
Figure 4. The lift is proportional to the model weight and the
maneuver load factor: Gs. In level flight, the lift is equal to the
model weight.
The stress in the spar depends on the spar-cap cross-section area
and the depth of the wing. Stress is defined as the load per unit
area—pounds per square inch in the US.
Let’s apply the scaling laws for a model twice the size. Lift is a
function of weight, and that increased 9 times. The effective span,
LE, and spar depth D are a function of size, and that doubled. The
spar area is size squared; that increases by 4 times.
Therefore, the stress factor is (2 x 9)/(2 x 4) = 2.25.
Working all of this out, you can see that when we double the
model size, the spar stresses are slightly more than double. Since the
allowable stress, or strength, of balsa is fixed (although it does vary
with density), you need a spar material with twice the strength, such
as spruce. This is why you can’t use balsa for spars on larger models
(and you can’t use spruce on even bigger airplanes).
So we have learned that as size increases, we must use stronger,
and therefore heavier, materials to carry the loads. This is one of the
reasons why airplanes actually get heavier by somewhat more than
span3—a factor of 8—each time they double in size; it’s closer to
span3.2—9 times. You can see this in the trend line through the data
from the table overleaf.
Is this real? The Boeing 747 fits on the same trend as the models,
in Figure 5, so there must be something to it, although there are other
factors driving the trend above size cubed. These laws apply in both
directions, so now you can see why the smaller indoor models can
be constructed from rather weak materials such as thin Styrofoam
sheet and lightweight balsa.
Wing Loading, Speed, and Energy: Now we know that airplanes get
disproportionately heavier with size, but what about the other
44 MODEL AVIATION
12sig2.QXD 10/25/04 10:33 AM Page 44
Figure 5
I’ll set a somewhat arbitrary ground rule that the propeller
diameter will be 20% of the span. This generally matches
experience, so it is a good starting point. This is important
because power required to produce a given thrust is proportional
to the propeller loading, which is conventionally known as disk
loading in the helicopter industry; it is the measure of thrust
divided by propeller swept area, or
The ideal, or theoretically minimum, power for a given thrust
and disk loading is
In the preceding, is the density of air—0.0023—at sea level,
thrust is in pounds, disk loading is in pounds per square foot, and
power is horsepower. Power required for a given thrust increases
with disk loading. Stated another way, smaller propellers require
more power for the same thrust. Let’s examine what happens to
these factors as we double the model’s size.
Since to hover, thrust equals the weight, power increases by
the same 9 times as thrust, multiplied by the square root of disk
loading. As shown in the preceding, disk loading increases by the
same factor as wing loading—2.25—and the square root of 2.25 is
1.5. So when you double the model size, the power required to
hover increases by 9 x 1.5, or 13.5.
Engine Capacity: While analyzing current 3-D aerobatic models,
I identified the engine capacity recommended by the
manufacturer. Plotting the size trend with capacity, I found that
the recommended capacity increases by 14.7 times when the
wingspan is doubled! This is quite a bit more than the 13.5
increase in power. Something else is going on here: another
scaling law!
In the world of full-scale aircraft, the results of a design
exercise are markedly driven by the ground rules. There is another
design ground rule with all RC aerobatic models, and that is a
noise limit. The larger models have to make compromises to meet
this requirement.
We already know that flight speed increases with size, so the
tip speed must decrease by the amount that the flight speed
increases. But the bigger model also has a bigger propeller, and at
the same rpm there would be a tip-speed increase. Consequently,
the rpm must be reduced by both of these factors.
In piston-engine technology, power increases with rpm, within
mechanical limits. Therefore, restricting—or actually reducing—
the maximum rpm limits the specific power (power per cubic
inch, or cc) for larger engines (which also tend to be lower
specific-power gas burners).
The model designers compensate by using proportionally
larger engines. Cranking (oops) this effect into the size trend
Figure 4. Spar Stress Relationship to Wing Lift
December 2004 45
One of the primary factors in noise generation is the
propeller—specifically the propeller tip speed. As the tip speed
approaches some fraction of the speed of sound (which is 1,100
feet per second at sea level), the noise increases noticeably. The
actual airspeed at the propeller tip is the vector sum of the
rotational speed (rpm multiplied by the propeller radius) and the
model flight speed:
12sig2.QXD 10/25/04 10:33 AM Page 45
46 MODEL AVIATION
results in the required capacity increasing by the higher 14.7
times for a double-size model.
Maximum Speed: You have seen that the scaling laws drive us to
disproportionately more power as we increase the model size, so
it should be no surprise that this power increase allows the larger
model to go faster.
The typical RC model’s theoretical maximum speed is set by
power and aerodynamic drag. For our “overpowered” models, the
drag at maximum speed is predominantly from wetted area, skin
friction, and form factor, or streamlining.
We conventionally express this drag in terms of the drag
coefficient, or Cd. Drag is related to Cd by a reference area.
Multiplying the Cd by the reference area and multiplying that by
the dynamic pressure calculates the drag. It looks like the
following formula, where the units are pounds, feet, and feet per
second.
For an airplane, the reference area—A—is conventionally the
wing area. Notice that area multiplied by Cd is also an area.
This is sometimes called the “equivalent flat plate drag area,”
because a flat plate with this area, placed perpendicular to the
airstream, would produce roughly the same drag.
Using this concept allows you to estimate the effects of design
changes such as retracting the landing gear, where you would
subtract an area equivalent to the landing-gear frontal area from
the initial equivalent flat plate drag area.
For a given geometry, Cd remains constant with size changes
(excepting the effects defined by that other scaling law discovered
by the good Doctor Reynolds, but we will ignore this for now).
For a given power and drag we can calculate the airspeed
using the following formula, where V is in feet per second and
drag is in pounds.
Substituting the preceding formula for drag, we get the
following, where A is in square feet.
Now you can estimate the effect of doubling size on maximum
speed. When you double the size of the model, the wing area—
and therefore the drag area—increases by 4 times. From my prior
investigation where I doubled the size, the power increased by
13.5 times. Now you see that the speed increase will be
proportional to the cube root of 13.5/4. The speed-increase factor
will be:
So when size increases by a factor of 2, the theoretical
maximum speed increases by a factor of 1.5, which is 50%. I have
called this speed increase “theoretical” because in practice there is
another limiting factor: the propeller. In an aerobatic model,
particularly one that is geared toward 3-D maneuvers, select a
propeller that is aimed at maximizing the hover and low-speed
performance.
Propellers only work well in a narrow speed range. Hover
propellers don’t work at speed. However, if we changed the
propeller for one that optimizes at the maximum speed,
specifically one with the correct smaller diameter and higher
pitch, we should be able to come close to demonstrating the speed
prediction. But propellers are a subject for another time.
Table 2 is a summary of the various scale effects when
doubling a model size or designing a model of a particular scale.
To calculate for a specific scale using a scientific calculator, first
calculate the scale factor as a fraction of roughly the scale in %
divided by 100 (or divide the new span by the baseline).
Second, raise that number to the exponent shown by pressing
the button for xy then pressing the number of the exponent from
the table. The result is the scaling factor you use to multiply the
parameter from your baseline model.
Applying these factors to the 24-inch, 5-ounce balsa
Staudacher and estimating the weight of a 96-inch model:
Weight is 5 x (96/24)3.22 or 5 x 43.22, which is 5 x 86.8 = 434
ounces, or 27 pounds.
Happy scaling. MA
Dave Harding
4948 Jefferson Dr.
Brookhaven PA 19015
Table 2
12sig2.QXD 10/25/04 10:34 AM Page 46
Edition: Model Aviation - 2004/12
Page Numbers: 43,44,45,46
December 2004 43
AT OUR FLYING field awhile ago I met a prospective member
who was waiting for one of our instructors, to have a session with
his 40-size trainer on dual control. He explained that this was his
second model; the first was destroyed when he flew it through a
tree.
While waiting, he watched two club members flying their
electric park flyers, and a funny look appeared on his face. He
realized that he could be learning the basics of flight control on a
much smaller, less-expensive airplane—one that flew slowly
enough to allow errors and recovery without the expense involved
in making the same mistakes on the conventional trainer.
One of the park flyers was also learning—and doing it solo. He
made repeated dunks into the long grass beyond our runway. Each
time the result was his picking up the model, adjusting the wing,
and launching again for another flight. How could that be? The
bigger airplane would almost be destroyed with such handling.
What was going on?
Scaling laws.
Among all of the wonderful laws of physics that bind our
universe are sets of principles known as scaling laws. These are the
relationships that define the effects that size have on physical
behavior. They are fundamental to our hobby and to our everyday
lives.
The primary set of scaling laws of interest to us are sometimes
known as “square-cube” laws, and their first part relates to how an
object’s surface area and volume vary with its size.
Area, Volume, and Weight: An object’s surface area is
proportional to the square of the size. If we double the size, we
increase the surface area by 2 squared: 22 = 4 times. This is true
regardless of the object’s shape.
The volume of this same object, when doubled in size,
increases by 2 cubed: 23 = 8 times. This is also true regardless of
the shape; hence, square-cube laws. Figure 1 depicts these
relationships.
So how is this relevant to our hobby? Bigger models are
heavier than smaller models, judging by much the same factors.
What I am about to explain is simplified to aid in the
understanding of the basic physics; however, as I will show later, it
is close to the real-world application. In fact, the following are the
methods we use in full-scale airplane design.
I’ll begin with a simple example: a solid-balsa model in which
the weight comes entirely from the structure. Let’s assume that we
make a 24-inch-wingspan model of a Staudacher aerobatic model
that weighs 5 ounces. We like it so much that we make a 48-inch
model. Wow! It weighs 40 ounces!
If the 24-inch model weighed 5 ounces and I doubled the size,
I should increase the volume by 2 x 2 x 2 = 8 times. And since I
am still using solid balsa, the density is the same, so the weight
varies by the volume—8 x 5 = 40 ounces. This is depicted in
figure 2.
Great! The scaling laws work. How would a really big model
look? Let’s use twice the 48-inch airplane, or a 96-inch-span
model. Doing the math (2 x 2 x 2 = 8 times), 8 x 40 = 320
ounces, or 20 pounds. That is about right for a big aerobatic
model.
But what if you are not interested in a solid-balsa airplane?
You want to put controls and power in it too. Let’s look at some
real aircraft. Table 1 includes a set of 3-D and aerobatic models
ranging from a light indoor/park flyer to a monster 40%, 122-
inch-span Staudacher.
These airplanes contain all that is necessary for them to fly
under our control. They also have the appropriate structure for
their weight and performance. I plotted them, as shown in Figure
3, to see if there was a trend or relationship between weight and
size.
Figure 1. Scaling Effects on Size, Area, and Volume
Table 1. A family of aerobatic models of increasing size
by Dave Harding
Illustrations by the author
Model
Type
Span—inches
Area—square inches
Weight—ounces
Wing loading—ounces per square foot
Minimum speed—feet per second
Energy—foot pounds
Todd
Long
Tiny
3D
24.0
225.0
3.6
1.4
9.0
1.0
Mountain
Models
Tantrum
3D
37.0
370.0
12.0
4.7
16.0
23.0
Gary
Wright E3D
3D
48.0
600.0
48.0
11.5
24.0
93.0
Magic ARF
3D
52.0
725.0
56.0
11.1
24.0
126.0
Excite
Aerobat
61.0
1,100.0
112.0
14.7
28.0
332.0
Eclipse
Aerobat
79.0
892.0
160.0
25.8
37.0
836.0
Lanier
Edge 540T
Aerobat
90.0
1,474.0
296.0
28.9
39.0
1,731.0
Hangar 9
Extra 300L
Aerobat
97.0
1,750.0
384.0
31.6
41.0
2,453.0
Lanier 40%
Staudacher
Aerobat
122.0
2,474.0
592.0
34.5
42.0
4,124.0
12sig2.QXD 10/25/04 10:33 AM Page 43
factors? Wing loading also increases with size, unless you
deliberately design to reduce it, but that puts you on another trend
line for lighter models; increase them in size and the square-cube
laws apply.
Since weight increases by 9 times and area increases by 4
times, wing loading increases 2.25 times for each doubling of
size. The consequence of this is higher minimum airspeed.
Lift is a function of speed squared, so increasing the wing
loading by 2.25 requires speed to increase by the square root of
2.25—or 1.5—or 50%.
If we combine the effects of increased weight and increased
speed, we find that the kinetic energy in our flying airplane
increases by the astonishing amount of approximately 20 times
with the doubling of a model’s size! This is the energy that must
dissipate when your aircraft lands—or crashes.
Imagine the difference in impact between a 2-pound hammer
and a 40-pound sledgehammer! When your model crashes, this
energy must go somewhere—and much of it goes into breaking
the model! This is why park flyers only bounce.
Power: I started this analysis with a family of 3-D aerobatic
models, and the one essential maneuver for this class of airplane
is hovering flight; let’s examine the impact of scale on power
required to hover.
Figure 2. Effects of Size on Weight
Figure 3
The data plots on a straight-line trend (on log-log scales, but let’s
not get picky because this is the way we do it in the full-scale
world). We even get an equation for the relationship. This is what
we call a weight trend in airplane design.
The trend equation indicates that span and weight are not related
by the cube power (3), but by 3.22. This is 9 times for a model of
twice the size—not 8. Could this be another factor in the scaling
laws?
For a start, we know from our experience that we need a stronger
structure as we build bigger models. Let’s see.
Stress: Lift is carried on the wing spars. The lift, which is
distributed over the wing, causes stress in the wing-spar caps. For
now, just let’s say that stress is a function of the lift and span. See
Figure 4. The lift is proportional to the model weight and the
maneuver load factor: Gs. In level flight, the lift is equal to the
model weight.
The stress in the spar depends on the spar-cap cross-section area
and the depth of the wing. Stress is defined as the load per unit
area—pounds per square inch in the US.
Let’s apply the scaling laws for a model twice the size. Lift is a
function of weight, and that increased 9 times. The effective span,
LE, and spar depth D are a function of size, and that doubled. The
spar area is size squared; that increases by 4 times.
Therefore, the stress factor is (2 x 9)/(2 x 4) = 2.25.
Working all of this out, you can see that when we double the
model size, the spar stresses are slightly more than double. Since the
allowable stress, or strength, of balsa is fixed (although it does vary
with density), you need a spar material with twice the strength, such
as spruce. This is why you can’t use balsa for spars on larger models
(and you can’t use spruce on even bigger airplanes).
So we have learned that as size increases, we must use stronger,
and therefore heavier, materials to carry the loads. This is one of the
reasons why airplanes actually get heavier by somewhat more than
span3—a factor of 8—each time they double in size; it’s closer to
span3.2—9 times. You can see this in the trend line through the data
from the table overleaf.
Is this real? The Boeing 747 fits on the same trend as the models,
in Figure 5, so there must be something to it, although there are other
factors driving the trend above size cubed. These laws apply in both
directions, so now you can see why the smaller indoor models can
be constructed from rather weak materials such as thin Styrofoam
sheet and lightweight balsa.
Wing Loading, Speed, and Energy: Now we know that airplanes get
disproportionately heavier with size, but what about the other
44 MODEL AVIATION
12sig2.QXD 10/25/04 10:33 AM Page 44
Figure 5
I’ll set a somewhat arbitrary ground rule that the propeller
diameter will be 20% of the span. This generally matches
experience, so it is a good starting point. This is important
because power required to produce a given thrust is proportional
to the propeller loading, which is conventionally known as disk
loading in the helicopter industry; it is the measure of thrust
divided by propeller swept area, or
The ideal, or theoretically minimum, power for a given thrust
and disk loading is
In the preceding, is the density of air—0.0023—at sea level,
thrust is in pounds, disk loading is in pounds per square foot, and
power is horsepower. Power required for a given thrust increases
with disk loading. Stated another way, smaller propellers require
more power for the same thrust. Let’s examine what happens to
these factors as we double the model’s size.
Since to hover, thrust equals the weight, power increases by
the same 9 times as thrust, multiplied by the square root of disk
loading. As shown in the preceding, disk loading increases by the
same factor as wing loading—2.25—and the square root of 2.25 is
1.5. So when you double the model size, the power required to
hover increases by 9 x 1.5, or 13.5.
Engine Capacity: While analyzing current 3-D aerobatic models,
I identified the engine capacity recommended by the
manufacturer. Plotting the size trend with capacity, I found that
the recommended capacity increases by 14.7 times when the
wingspan is doubled! This is quite a bit more than the 13.5
increase in power. Something else is going on here: another
scaling law!
In the world of full-scale aircraft, the results of a design
exercise are markedly driven by the ground rules. There is another
design ground rule with all RC aerobatic models, and that is a
noise limit. The larger models have to make compromises to meet
this requirement.
We already know that flight speed increases with size, so the
tip speed must decrease by the amount that the flight speed
increases. But the bigger model also has a bigger propeller, and at
the same rpm there would be a tip-speed increase. Consequently,
the rpm must be reduced by both of these factors.
In piston-engine technology, power increases with rpm, within
mechanical limits. Therefore, restricting—or actually reducing—
the maximum rpm limits the specific power (power per cubic
inch, or cc) for larger engines (which also tend to be lower
specific-power gas burners).
The model designers compensate by using proportionally
larger engines. Cranking (oops) this effect into the size trend
Figure 4. Spar Stress Relationship to Wing Lift
December 2004 45
One of the primary factors in noise generation is the
propeller—specifically the propeller tip speed. As the tip speed
approaches some fraction of the speed of sound (which is 1,100
feet per second at sea level), the noise increases noticeably. The
actual airspeed at the propeller tip is the vector sum of the
rotational speed (rpm multiplied by the propeller radius) and the
model flight speed:
12sig2.QXD 10/25/04 10:33 AM Page 45
46 MODEL AVIATION
results in the required capacity increasing by the higher 14.7
times for a double-size model.
Maximum Speed: You have seen that the scaling laws drive us to
disproportionately more power as we increase the model size, so
it should be no surprise that this power increase allows the larger
model to go faster.
The typical RC model’s theoretical maximum speed is set by
power and aerodynamic drag. For our “overpowered” models, the
drag at maximum speed is predominantly from wetted area, skin
friction, and form factor, or streamlining.
We conventionally express this drag in terms of the drag
coefficient, or Cd. Drag is related to Cd by a reference area.
Multiplying the Cd by the reference area and multiplying that by
the dynamic pressure calculates the drag. It looks like the
following formula, where the units are pounds, feet, and feet per
second.
For an airplane, the reference area—A—is conventionally the
wing area. Notice that area multiplied by Cd is also an area.
This is sometimes called the “equivalent flat plate drag area,”
because a flat plate with this area, placed perpendicular to the
airstream, would produce roughly the same drag.
Using this concept allows you to estimate the effects of design
changes such as retracting the landing gear, where you would
subtract an area equivalent to the landing-gear frontal area from
the initial equivalent flat plate drag area.
For a given geometry, Cd remains constant with size changes
(excepting the effects defined by that other scaling law discovered
by the good Doctor Reynolds, but we will ignore this for now).
For a given power and drag we can calculate the airspeed
using the following formula, where V is in feet per second and
drag is in pounds.
Substituting the preceding formula for drag, we get the
following, where A is in square feet.
Now you can estimate the effect of doubling size on maximum
speed. When you double the size of the model, the wing area—
and therefore the drag area—increases by 4 times. From my prior
investigation where I doubled the size, the power increased by
13.5 times. Now you see that the speed increase will be
proportional to the cube root of 13.5/4. The speed-increase factor
will be:
So when size increases by a factor of 2, the theoretical
maximum speed increases by a factor of 1.5, which is 50%. I have
called this speed increase “theoretical” because in practice there is
another limiting factor: the propeller. In an aerobatic model,
particularly one that is geared toward 3-D maneuvers, select a
propeller that is aimed at maximizing the hover and low-speed
performance.
Propellers only work well in a narrow speed range. Hover
propellers don’t work at speed. However, if we changed the
propeller for one that optimizes at the maximum speed,
specifically one with the correct smaller diameter and higher
pitch, we should be able to come close to demonstrating the speed
prediction. But propellers are a subject for another time.
Table 2 is a summary of the various scale effects when
doubling a model size or designing a model of a particular scale.
To calculate for a specific scale using a scientific calculator, first
calculate the scale factor as a fraction of roughly the scale in %
divided by 100 (or divide the new span by the baseline).
Second, raise that number to the exponent shown by pressing
the button for xy then pressing the number of the exponent from
the table. The result is the scaling factor you use to multiply the
parameter from your baseline model.
Applying these factors to the 24-inch, 5-ounce balsa
Staudacher and estimating the weight of a 96-inch model:
Weight is 5 x (96/24)3.22 or 5 x 43.22, which is 5 x 86.8 = 434
ounces, or 27 pounds.
Happy scaling. MA
Dave Harding
4948 Jefferson Dr.
Brookhaven PA 19015
Table 2
12sig2.QXD 10/25/04 10:34 AM Page 46